上 ダイヤモンド構造 充填率 計算 226890-ダイヤモンド構造 充填率 計算

空間が原子の球によって占められる割合を充填率といいます。 (1) 面心立方構造（最密充填） ダイアモンド構造 の充填率を計算してください。 0740 2 2 3 4 1 3 3 3 u r Sr (2) 体心立方構造 (3） ダイヤモンド構造3 3 × 1 8 ×8 1 2 ×6 ÷𝑎3× 球の空間占有率 ＝74％ 3a 4𝜋 3 4 𝑎 3 3 1 8 ×81 ÷𝑎3 球の空間占有率 ＝68％ 5 球を平面に敷き詰めると，最密充填構造は図1(a)のようになり，球 ①の周りには球②～⑦が接する。ダイヤモンド型構造 ダイヤモンドでは，結合を4つ持ったテトラポッド型の炭素原子どうしが 共有結合で結合し，立体的な網目構造を作っている．炭素原子はsp3混 成状態を取っている．その他に，Si，Geもダイヤモンド型構造を取る．

トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

ダイヤモンド構造 充填率 計算

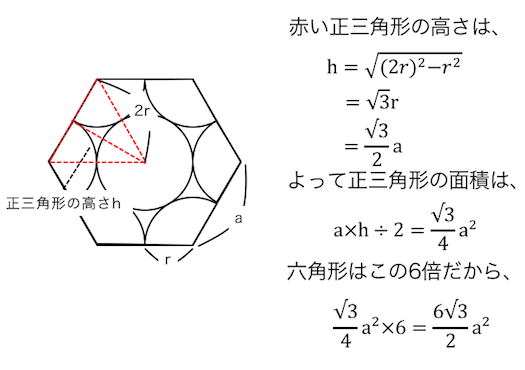
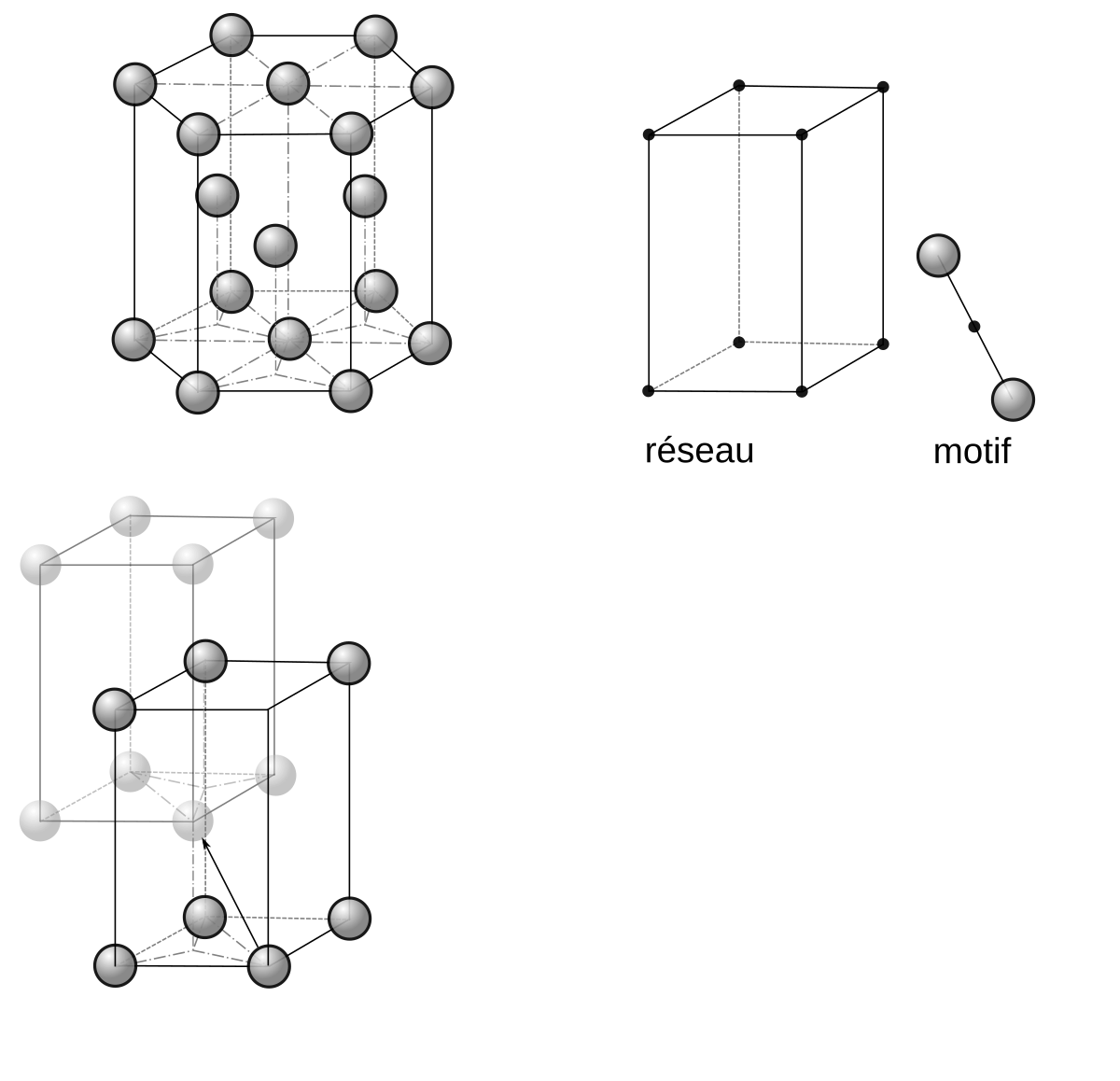
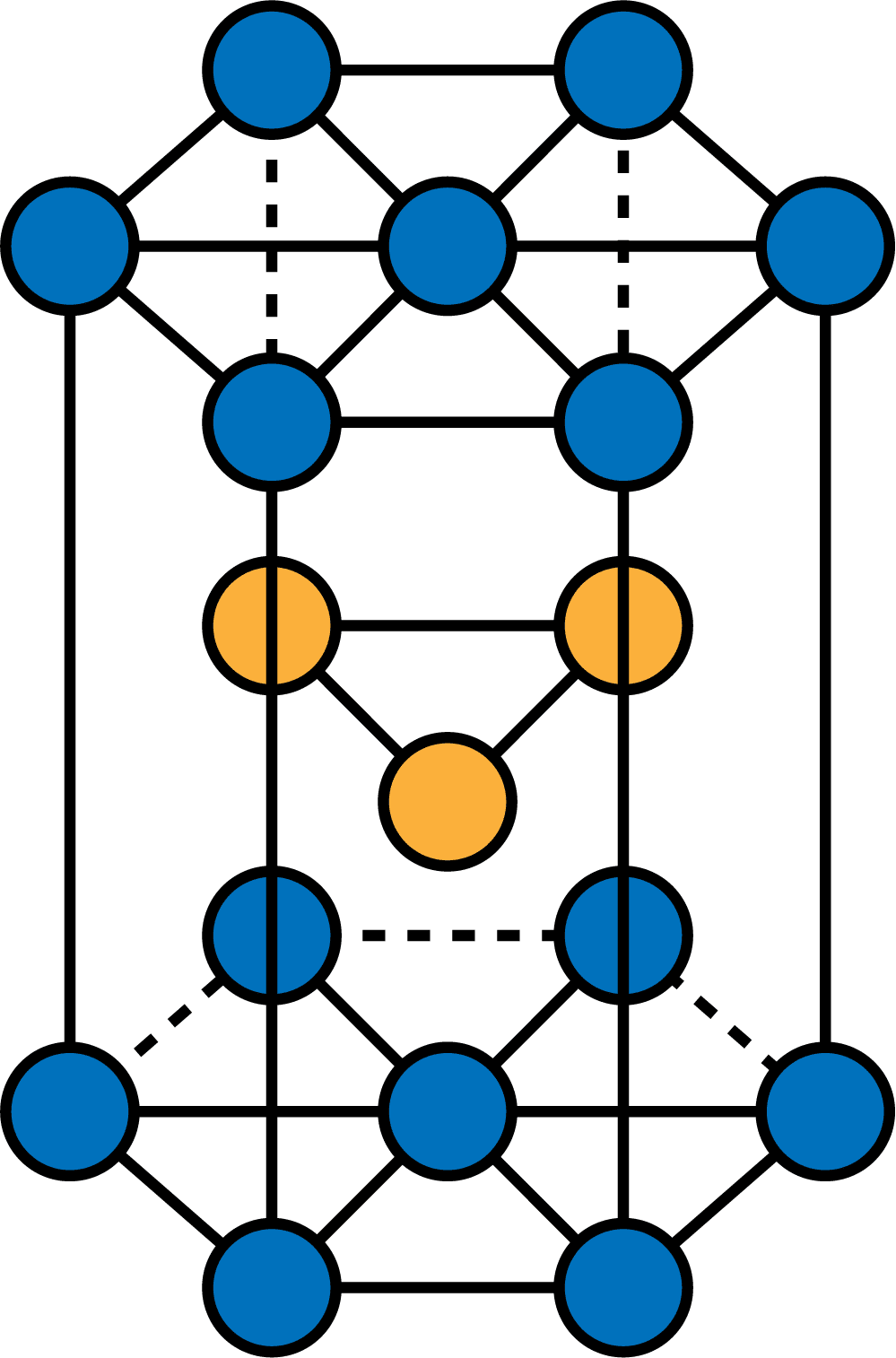
ダイヤモンド構造 充填率 計算-問題2－4 ハニカム構造 ハニカム構造とは、平面上にセル壁がミクロ形状を成して周期的に配列する構造であり、 例えば、下図のようにセル形状が六角形の場合を六方セル構造と呼ぶ。本課題では、有限 要素法を用いてハニカム構造の力学特性を求めたい。六方最密構造（hcp hexagonal closedpacked) 体心立方格子(bcc body centered cubic) ダイヤモンド構造 最密充填構造 配位数＝12 最密充填構造 配位数＝12 配位数＝8 配位数＝4 sp3 混成軌道の4ボンドの制約下で最密充填 最近接原子距離 = 第2最近接原子距離 = a

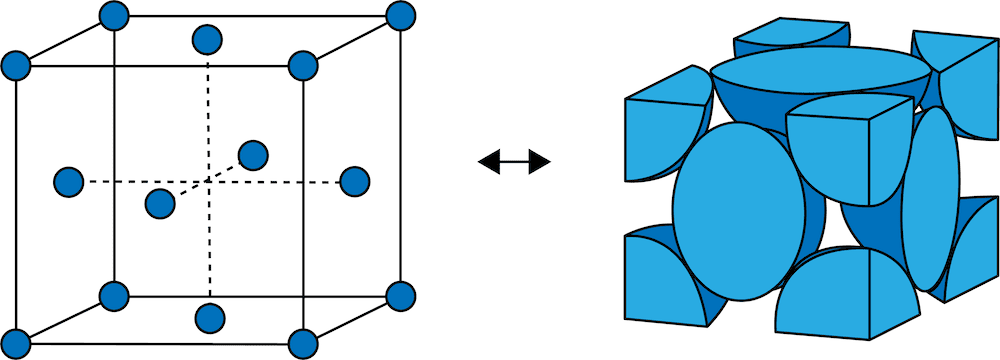
面心立方格子とは 配位数や充填率 密度 格子定数 半径などを解説 化学のグルメ

物理： 球の充填を計算する 08年5月29日 Nature 453, 7195 容器に最も効率よく球を詰める方法を探すことは、非常に古くからある数学パズルの1つである。この問題は、粉粒体処理、果物の箱詰め、コロイドのふるまい、生細胞などさまざまな系に実際的な関連空間充填率： (単位胞中の原子数)×(1原子当たりの 体積)／(単位胞自身の体積)と定義。同 一原子からなる最密充填構造の結晶の 空間充填率は である。 実験的にはホウ素の共有結合結晶も 合成されており，00 年代から，多く の多型が見つかってきた。これより、ダイヤモンド c の充填率は、約 34% と隙間の多い構造であることが分かります。 また、ダイヤモンド C の密度は、アボガドロ定数を N A 、体積を a 3 cm 3 、原子量を 12 とすると、次のようになります。

計算の詳細は文献(7)に 記載してある。 4結 果及び考察 41圧 力損失の解析解と数値解との比較 空間率が一定の充填層の圧力損失に関しては,一般 にErgun式 が利用される。しかしながら液体クロマ トカラムでは,充填層の局所空間率が流れ方向に変化となり、これを用いて充填率apfを計算すると、 となる。 各種の構造における充填率 同様の方法を使えば、どの結晶構造についても空間充填率の理論値を求めることができる。一般的な構造については以下のような値である（小数点以下3位で四捨五入）。ダイヤモンド格子の充填率を計算する方法 科学 ;

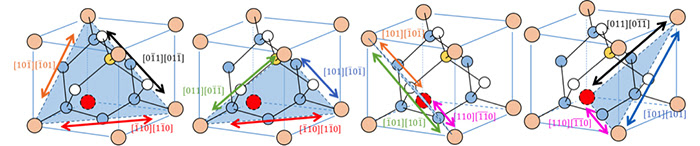
図12 岩塩型構造結晶構造 図11 閃亜鉛鉱型構造の結晶構造 図10 底面に投影されたダイヤモンド 型構造の原子位置 分数は立方体の稜を単位とした底面 からの高さを示す。0 と1/ 2 の点はfcc 格子上にある。1/ 4 と3/ 4 にある点も、 体対角線沿いに/ だけずれたfcc物理： 球の充填を計算する 08年5月29日 Nature 453, 7195 容器に最も効率よく球を詰める方法を探すことは、非常に古くからある数学パズルの1つである。この問題は、粉粒体処理、果物の箱詰め、コロイドのふるまい、生細胞などさまざまな系に実際的な関連ダイヤモンド型構造において、交互に 空間が原子の球によって占められる割合を充填率といいます。 (1) 面心立方構造（最密充填） (2) 体心立方構造 (3) ダイアモンド構造 の充填率を計算してください。

ダイヤモンドの充填率の出し方がわかりません 答えは34 となるようで Yahoo 知恵袋

暗記不要 ダイヤモンドの密度の求め方をまとめてみた 化学受験テクニック塾

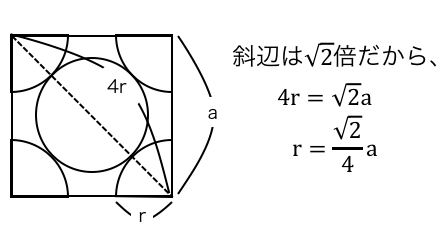
充填率 原子の体積 最密構造の体積 充 填 率 = 原 子 の 体 積 最 密 構 造 の 体 積 × 100 = 4 3 π r 3 × 6 24 2 r 3 × 100 = 74 ( %) 最密構造の体積に関してはSTEP2で求めた値を使う。 また、球の体積は4/3πr 3 と表すことができる（これは数学の知識）ので、六方最密(f) ダイヤモンド型 ダイヤモンド C C 8個 — (g) 六方最密格子（hcp）マグネシウム Mg Mg 2個 — (f) — グラファイト C C 4個 — 3種類の立方格子の充填率を計算によって確かめよ。 (a) 面心立方格子（立方最密充填）74% (b) 体心立方格子 68%六方最密充填構造においても、同様に充填率を算出することができる。六角柱の一辺をa 、高さをc とおくと、 =, = となり、これを用いて充填率APFを計算すると、 = = (/) () / = ≈ となる。 各種の構造における充填率 同様の方法を使えば、どの結晶構造についても空間充填率の理論値を求める

ｈ29センター化学第1問 問2 単位格子に含まれる原子数 配位数 充填率の語呂合わせ 入試化学を語呂合わせで解く大学入試ゴロ化学

空間充填率 Wikiwand

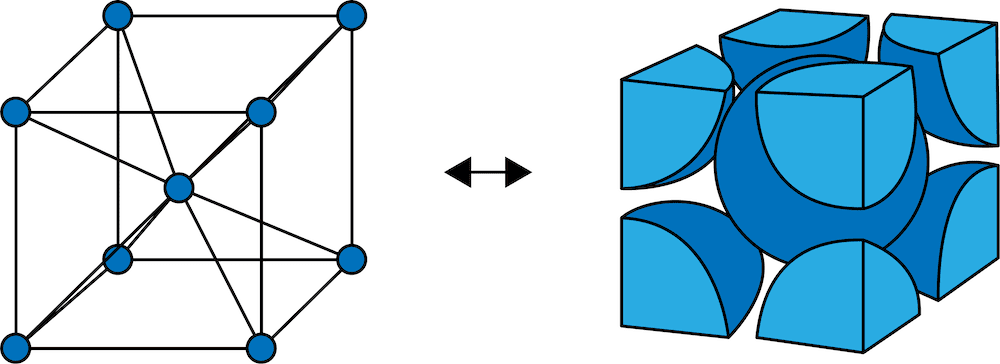
成分やダイヤモンド構造に関する構造評価手法として適 用されている。DLCの固体13C NMRスペクトルには、 sp2炭素由来のピークが136ppm付近に、sp3炭素由来の ピークが55ppm付近に観測される。DLC膜については、 サンプリングの困難さからその適用例は少ないが結晶⑧ ダイヤモンド型結晶格子の計算問題 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up Nextを示した．（b）は，bcc 構造で原子の位置が立方体の角（頂点）と中心にあることを示している． bcc 単位格子の充填率を計算するには，次式を使う． 充填率 ＝ 原子が占める体積 ／ 空間の全体積 × 100％

19センター化学 第1問 問2 単位格子 充填率の語呂合わせ 入試化学を語呂合わせで解く大学入試ゴロ化学

結晶化学

六方最密構造（hcp hexagonal closedpacked) 体心立方格子(bcc body centered cubic) ダイヤモンド構造 最密充填構造 配位数＝12 最密充填構造 配位数＝12 配位数＝8 配位数＝4 sp3 混成軌道の4ボンドの制約下で最密充填 最近接原子距離 = 第2最近接原子距離 = a成分やダイヤモンド構造に関する構造評価手法として適 用されている。DLCの固体13C NMRスペクトルには、 sp2炭素由来のピークが136ppm付近に、sp3炭素由来の ピークが55ppm付近に観測される。DLC膜については、 サンプリングの困難さからその適用例は少ないがダイアモンド構造の単位胞内の原子数は？ ダイアモンド構造の 年の最高 ダイヤモンド構造 充填率 新版 イメージ

ダイヤモンド型結晶の問題解法 覚えるべき事４選 化学受験テクニック塾

ダイヤモンド型構造 坂根弦太のdv Xa Venus日誌

19センター化学 第1問 問2 単位格子 充填率の語呂合わせ 入試化学を語呂合わせで解く大学入試ゴロ化学

5秒で充填率の求め方を理解 公式なんて要らない 化学受験テクニック塾

六方最密構造の密度 充填率 配位数全ての求め方をはじめから丁寧に 化学受験テクニック塾

発展問題 氷の構造など Shinshu Univ Physical Chemistry Lab Adsorption Group

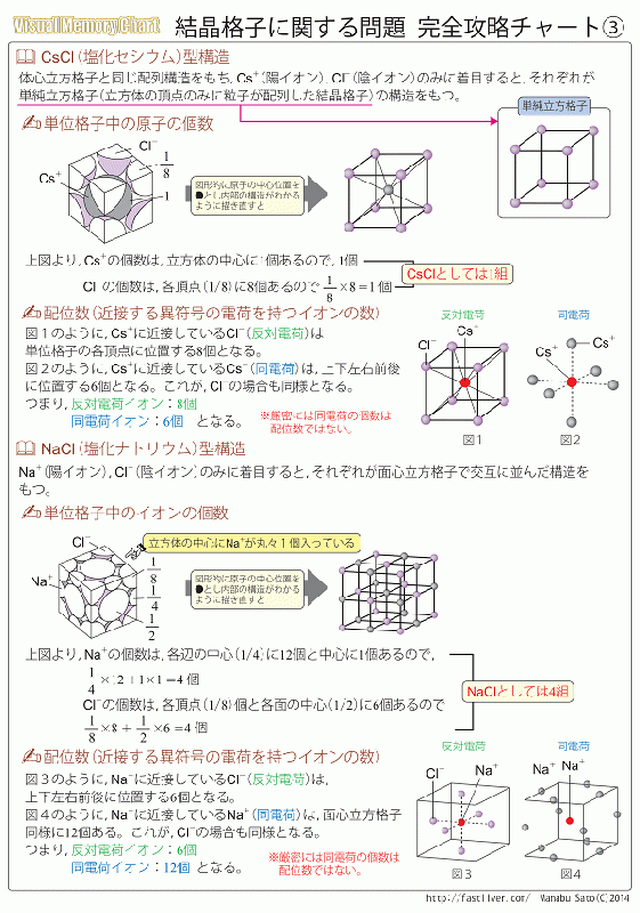
結晶格子に関する問題 完全攻略チャート 過去問解説集 自宅でできる受験対策ショップ ワカルー Wakaru

トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

19センター化学 第1問 問2 単位格子 充填率の語呂合わせ 入試化学を語呂合わせで解く大学入試ゴロ化学

19センター化学 第1問 問2 単位格子 充填率の語呂合わせ 入試化学を語呂合わせで解く大学入試ゴロ化学

トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

ダイヤモンドの充填率の出し方がわかりません 答えは34 となるようで Yahoo 知恵袋

高校理論化学 共有結合の結晶 ダイヤモンドの結晶構造 受験の月

ダイヤモンドの結晶の単位格子において充填率が面心立方格子の充填率のち Yahoo 知恵袋

金属の結晶格子を仕組みから徹底解説 受験メモ

トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

ねがてぃぶろぐ Akaikkrでダイヤモンド型構造半導体

粉末材料の結晶構造を正確に解析可能に リートベルト法でより正確な格子パラメーターを得るには Academist Journal

ダイヤモンド型構造 坂根弦太のdv Xa Venus日誌

結晶化学

トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

ダイヤモンド型結晶の問題解法 覚えるべき事４選 化学受験テクニック塾

高校化学基礎まとめ 金属結晶の充填率の求め方 Mm参考書

暗記不要 ダイヤモンドの密度の求め方をまとめてみた 化学受験テクニック塾

空間充填率 Wikipedia

結晶化学

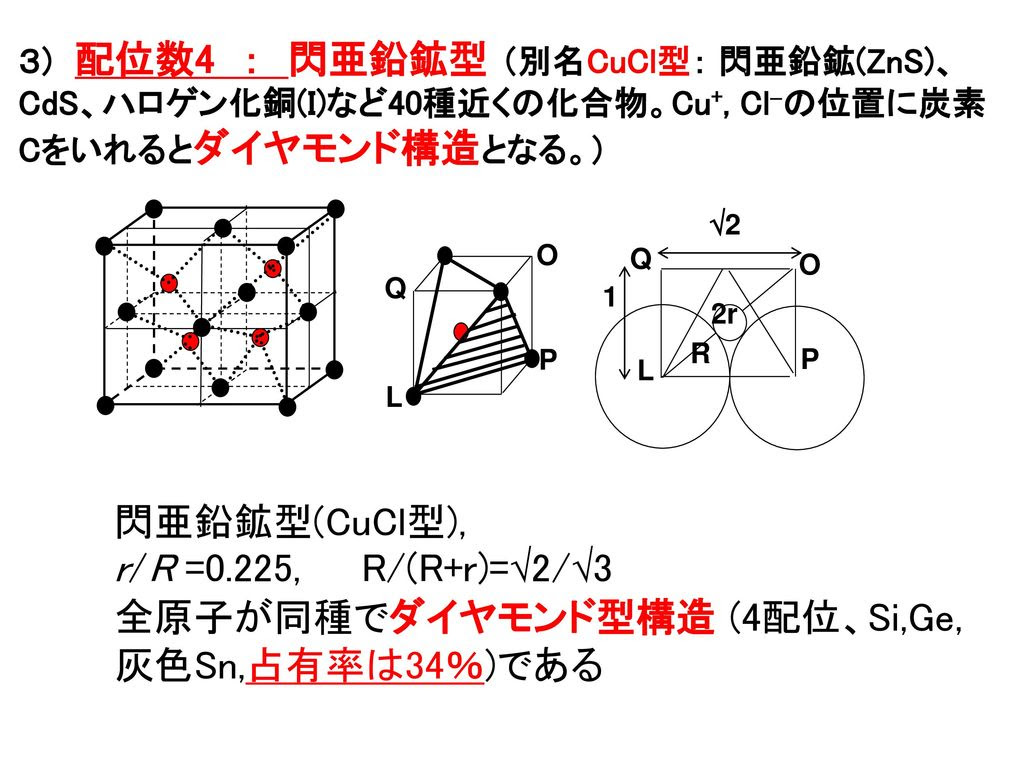
トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

ダイヤモンドの結晶の単位格子を図に示した この結晶格子は 面心立方格子の配列 Yahoo 知恵袋

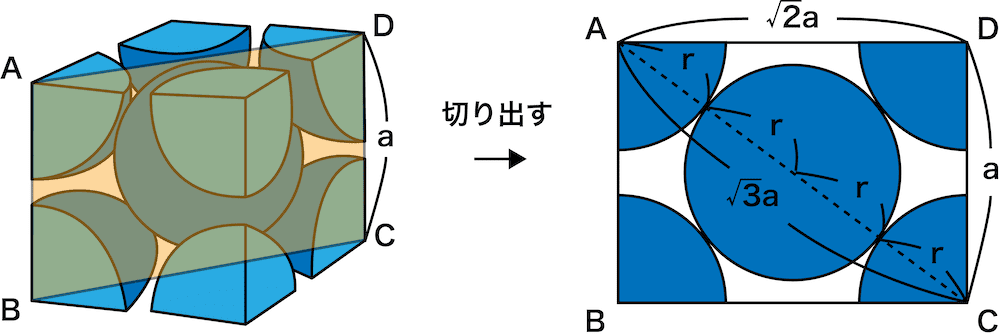
体心立方格子とは 配位数や充填率 密度 格子定数 半径などを解説 化学のグルメ

ダイヤモンド型結晶の問題解法 覚えるべき事４選 化学受験テクニック塾

面心立方格子とは 配位数や充填率 密度 格子定数 半径などを解説 化学のグルメ

ダイヤモンド型構造の原子半径と単位格子の関係 Youtube

ダイヤモンド型結晶の問題解法 覚えるべき事４選 化学受験テクニック塾

トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

シリコンはダイヤモンド構造をとり 格子定数はa 5 43aで Yahoo 知恵袋

結晶化学

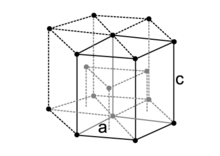
六方最密充填構造 Wikipedia

暗記不要 ダイヤモンドの密度の求め方をまとめてみた 化学受験テクニック塾

暗記不要 ダイヤモンドの密度の求め方をまとめてみた 化学受験テクニック塾

高校理論化学 その他のイオン結晶 Caf Sub 2 Sub 型 Zns型構造 受験の月

高校理論化学ダイヤモンドの充填率について 写真のように一辺の長さをaと Yahoo 知恵袋

ダイヤモンド型結晶の問題解法 覚えるべき事４選 化学受験テクニック塾

六方最密構造の密度 充填率 配位数全ての求め方をはじめから丁寧に 化学受験テクニック塾

ダイヤモンド型結晶の問題解法 覚えるべき事４選 化学受験テクニック塾

ダイヤモンドの充填率の求め方を教えてください 一辺は3 56 10 8cm Yahoo 知恵袋

六方最密構造とは 単位格子に含む原子数や配位数 高さ 充填率の求め方など 化学のグルメ

19センター化学 第1問 問2 単位格子 充填率の語呂合わせ 入試化学を語呂合わせで解く大学入試ゴロ化学

体心立方格子とは 配位数や充填率 密度 格子定数 半径などを解説 化学のグルメ

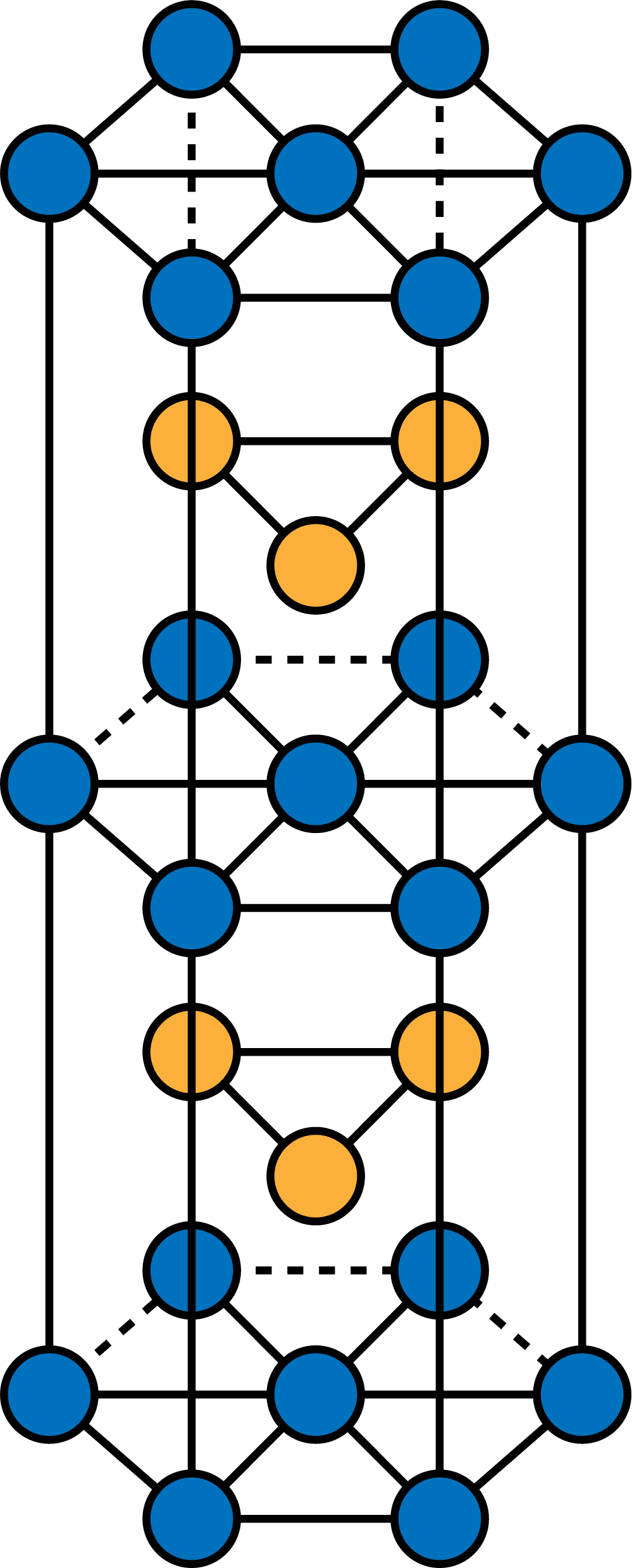
六方最密構造とは 単位格子に含む原子数や配位数 高さ 充填率の求め方など 化学のグルメ

化学画像はダイヤモンドの結晶格子なのですが 2a 4rとできないの Yahoo 知恵袋

ダイヤモンド型結晶の問題解法 覚えるべき事４選 化学受験テクニック塾

結晶化学

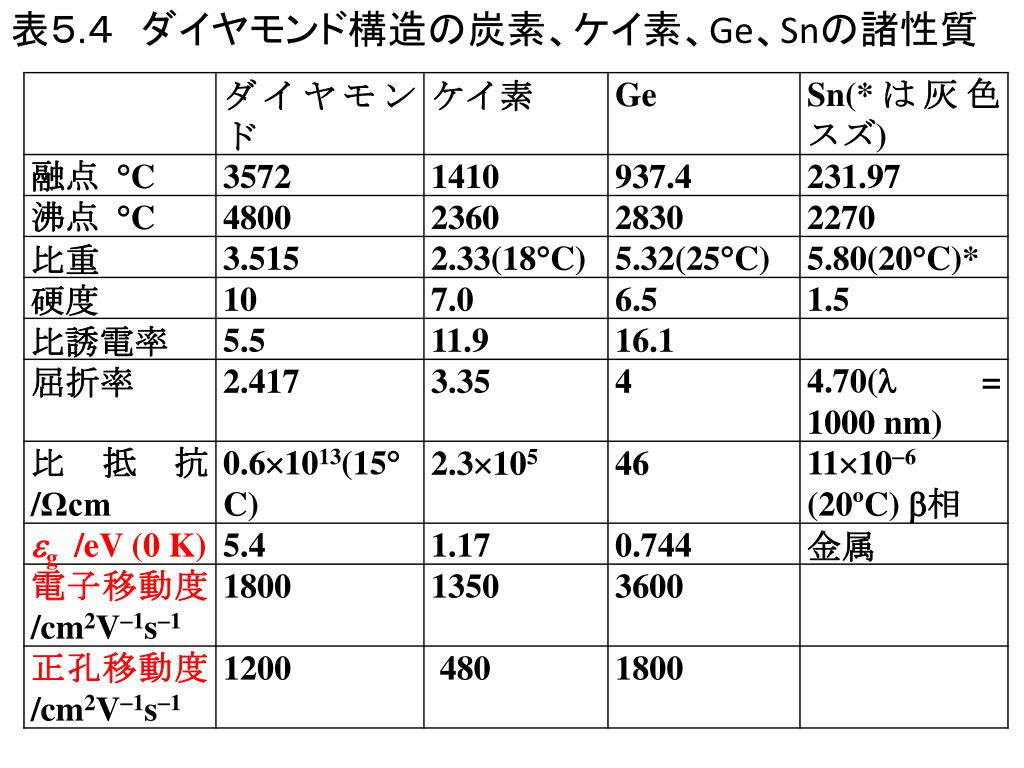
トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

ダイヤモンド型結晶の問題解法 覚えるべき事４選 化学受験テクニック塾

ダイヤモンド構造の面間隔について質問があります 格子定数をaとした場合の Yahoo 知恵袋

六方最密構造の密度 充填率 配位数全ての求め方をはじめから丁寧に 化学受験テクニック塾

結晶化学

ダイヤモンドの単位格子の密度を求める過程の式なのですが 写真の 3 Yahoo 知恵袋

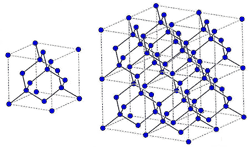
トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

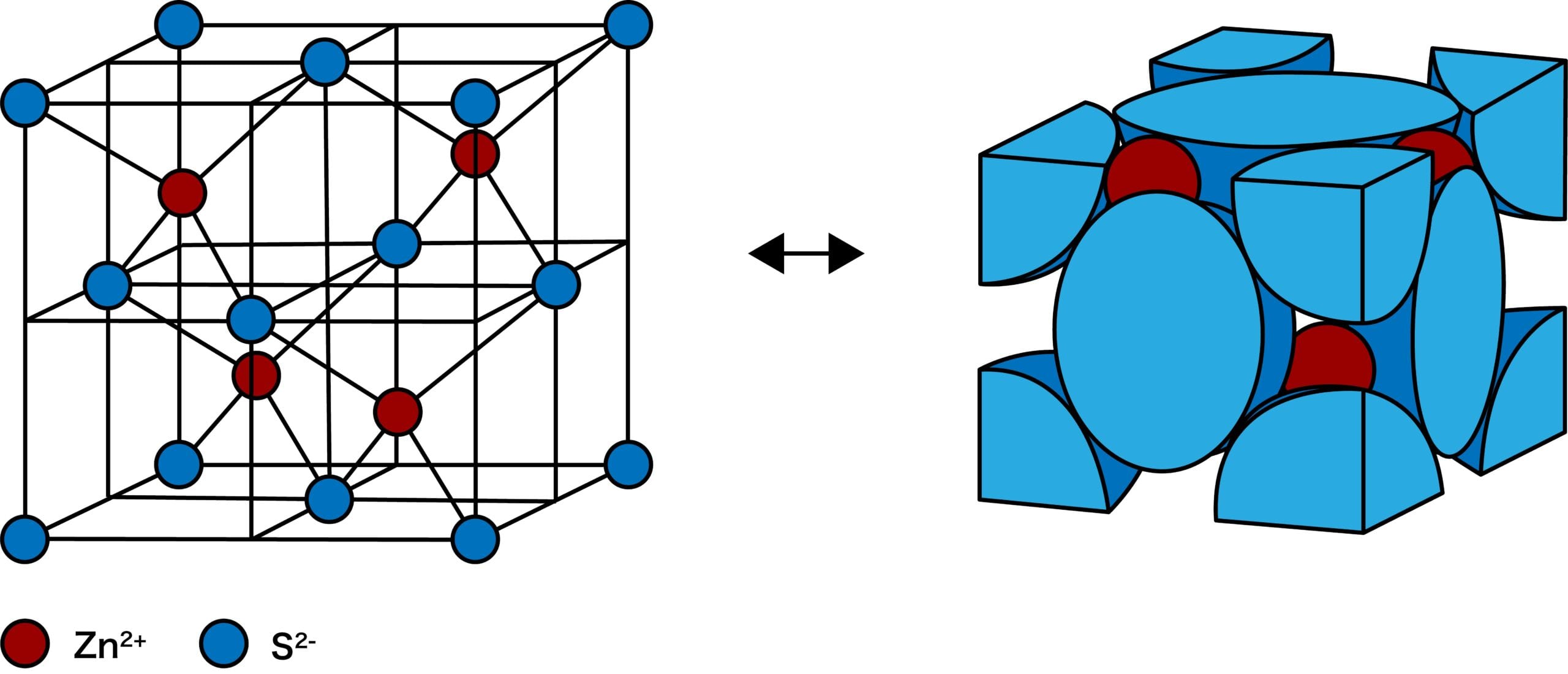
トップレート ダイヤモンド構造 充填率 人気のある画像を投稿する

空間充填率 Wikipedia

六方最密構造とは 単位格子に含む原子数や配位数 高さ 充填率の求め方など 化学のグルメ

Incoming Term: ダイヤモンド構造 充填率 計算,